Table of Contents
RESINC - Remote sensing of aerosols, clouds, and trace gases using synergy of AATSR, MERIS, and SCIAMACHY
Documents
Idea
Use spectral importance sampling method (mc_spectral_is) to simulate high resolution SCIAMACHY spectra (NO2 channel 425-470 nm).
Calculations in directory
/usr/users/emde/projects/resinc/
SCIAMACHY
- typical nadir spatial resolution: 30km x 60km (along/cross track)
- S/N ratio for hyperspectral measurements 600 acc. to Alex
- NO2 channel: 425-470 nm, FMHM (Gaussian) 0.44
To do
- VROOM with different geometry
- 3D calculation in nadir geometry
Molecular optical thickness file
The directory write_molecular_tau includes a script that generates a molecular_tau_file for 425-470 nm from the uvspec verbose output.
This script has been validated by comparing disort clear sky calculations with and without molecular_tau_file.
(In order to get accurate results the output format of the verbose output needed to be changed. → now committed)
The spectral resolution of the molecular_tau_file and hence of all calculations is 0.1 nm, resulting in 451 spectral points.
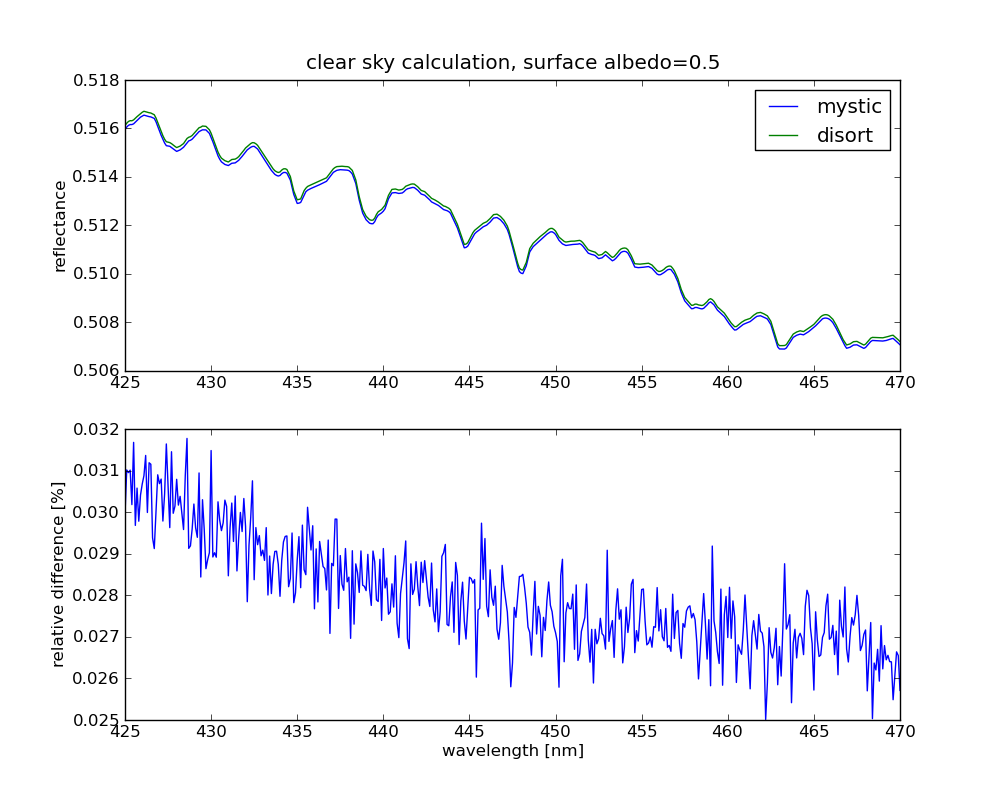
Clear sky test with high surface albedo
For this test the surface albedo was set to a high value (0.5) so that the NO2 absorption features are well visible.
- calculation wavelength: 450 nm
- number of photons: 1e6
- CPU time: 3m 24s
- standard deviation at 450 nm: 0.04%
- CPU time DISORT: 24s
<columns>
<newcolumn>
</columns>
The noise in the relative difference is disort noise ![]() For 1e6 photons (and also 1e8 photons) there is a spectral dependence in the relative difference. Not corrected is the spectral dependence of the Rayleigh depolarisation factor, but this is too small to explain this spectral dependence. The calculation with 1e9 photons shows that the spectral dependence is a statistical error which vanishes when a sufficient number of photons is used. Still it is not proven that the method also works correctly with cloud or aerosol scattering (importance sampling of total phase matrix and total single scattering albedo).
For 1e6 photons (and also 1e8 photons) there is a spectral dependence in the relative difference. Not corrected is the spectral dependence of the Rayleigh depolarisation factor, but this is too small to explain this spectral dependence. The calculation with 1e9 photons shows that the spectral dependence is a statistical error which vanishes when a sufficient number of photons is used. Still it is not proven that the method also works correctly with cloud or aerosol scattering (importance sampling of total phase matrix and total single scattering albedo).
Moved importance sampling of single scattering albedo from escape_probability to scattering. Clearsky still works and the calculation time remains the same.
Tests with 1D cloud, Heney-Greenstein
Common settings for all following cloud tests:
- cloud altitude: 1-2 km
- effective radius: 10 um
- HG phase function: g=0.85, ssa=1 (constant for all wavelengths)
- surface albedo: 0.1
Cloud tau=3
<columns>
- calculation wavelength: 450 nm
- number of photons: 1e6
- CPU time: 11m 42s; memory: 898 MB, CPU 1wvn: 42s, 17m with phasecorr
- standard deviation at 450 nm: 0.3%
- CPU time DISORT: 28s, memory: 976 MB
<newcolumn>
</columns>
Cloud tau=10
<columns>
- calculation wavelength: 450 nm
- number of photons: 1e6
- CPU time: 39m 59s memory: 900 MB, CPU 1wvn 2m 18s , with phasecorr 40m 12s (strangely no time difference between 2 methods???)
- standard deviation at 450 nm: 0.25%
- CPU time DISORT: 27s, memory: 976 MB
There is a spectral dependence in the relative difference between DISORT and MYSTIC. The correction of the calculation of the total phase function can be enabled or disabled. Something still wrong with spectral importance sampling of Rayleigh scattering????
<newcolumn>
</columns>
Cloud tau=20
<columns>
- calculation wavelength: 450 nm
- number of photons: 1e6
- CPU time: 81m 49s memory: 900 MB, CPU 1wvn 4m43s , with phasecorr 80 m(strangely no time difference between 2 methods???)
- standard deviation at 450 nm: 0.22%
- CPU time DISORT: 27s, memory: 976 MB
<newcolumn>
</columns>
Tests with 1D cloud, Mie phase function
Cloud tau=10
<columns>
- calculation wavelength: 450 nm
- number of photons: 1e6
- CPU time vroom nophasecorr: 16m 2s memory: 900 MB, CPU 1wvn 2m 18s
- CPU time novroom: nophasecorr 39m 54s
- standard deviation at 450 nm: 0.01%, without vroom 2.2% → spikes can follow and increase these values
- CPU time DISORT: 35s, memory: 3.6GB
- CPU time with vroom and approx exponential function exp(x) ~ 1+x: 14m 26s, saves less than 10%, so the approximation is not worth implementing!
VROOM does not work with phasecorrection yet. phasecorrection currently in scattering_probability_tot, which is without vroom only used before local estimate, with vroom in many other places, so I don't know what happens …
<newcolumn>
</columns>
Tests with cubic clouds
<columns>
- SZA: 32°
- calculation wavelength: 450 nm
- number of photons: 4e7
- CPU time: ???
- vroom, Mie
<newcolumn>

</columns>
<columns>
- Test with szs=5
- 1e7 photons, 4 sample pixels
- vroom, Mie
- CPU time: 78 min 50 s
<newcolumn>

</columns>